[ENGLISH]

 

人的绩效和认知的数学建模

 

Dr.Changxu Wu

 

[特点]      [理论框架和模型]     [建模视频教程]      [设计工具]

 

 

 

本站的目的是总结和整合基于排队网络的所有数学建模工作。它也是人的绩效的数学建模学习资料平台。

 

1. 人的绩效和认知的数学建模的特点

 

数学方程式可以严格地预测，量化和分析人类绩效，工作负荷，脑电波和其他人类行为指标。与计算机仿真相比，

 

1) 我们通过建立人类行为的数学模型和方程式通过变量的关系（包括每个方程的输入和输出之间的关系），能够比较深入地理解和清晰地量化人类行为的机制。读懂数学模型将比阅读上千行计算机代码相更加容易一些，也更容易理解和把握变量之间的关系和人的行为机制。

 

2) 人类行为的数学模型和方程可以相对大量计算机程序更容易地进行编辑、修改、改进和整合，从而推导出新的数学方程。

 

3) 人类行为和绩效的数学模型和方程可以相对容易地用不同的编程语言来实现，并且可以嵌入到不同的智能系统中与系统设计一起工作。

 

4) 数学模型和方程可以得到比仿真结果更精确的解析解。

 

5) 有一些数学模型和方程量化了整个人类认知系统（见整个网络中的方程式），这是数学建模方法的另一个独特之处。

 

6) 有一些数学模型和方程式可以通过数学推导直接证明，而无需通过实证数据进行验证（See Equations in Wu, C., Berman, M., & Liu, Y., 2010）

 

 

2. 数学模型和方程式在本总结网页中的使用

 

这里总结的公式也可以作为索引页和指南工具，供建模人员使用，他们可以：

 

1) 使用这些数学模型来量化和预测人类绩效中的新现象和新任务

 

2) 添加和开发新的方程式和数学模型，以量化人类认知和绩效的新成分，并随着人的信息加工排队网络模型（QN-MHP）的框架进一步发展

 

3) 用于和嵌入到不同的智能系统和工具设计中，对人类绩效和行为进行预测

 

 

3. 学习教程和免费会员资格:

1)     如何建立和验证人类绩效模型（概述）（Wu，建模中的五个关键问题）（视频） [PDF]

 

2)     如何建立数学模型（例如第9-10页）（Wu & Liu，2008a）（学习视频请联系Dr.Changxu Wu：changxu.wu@gmailcom）

 

3)     如何在人类绩效建模中整合和建立新的数学模型 (Zhang & Wu, 2017)

 

4)     若想成为人类绩效数学建模小组的成员（用户或贡献者），获得相关的视频教程（如如何建模），请发送电子邮件至changxu.wu@gmailcom（请列出您的全名和机构/公司名称），我们将向您发送最新的更新、建模工作和教程。

 

 

3. 基于本页方程式的人机系统设计工具 coming soon [Link]

 

 

4. 以人的信息加工排队网络模型为框架的数学方程

 

 

人的信息加工排队网络模型的总体结构

 

 

服务器信息处理时间和信息处理容量

Server Name	Processing Timea: Exponential Distribution (Mean, Min) (ms)	Capacity (Entitiesa)		Server Name	Processing Time: Exponential Distribution (Mean, Min) (ms)	Capacity (Entitiesb)
1	Exp (42, 25)	4		5	Exp (42, 25)	2
2	Exp (42, 25)	4		6	Exp (42, 25)	1
3	Exp (42, 25)	4		7	Exp (42, 25)	1
4	Exp (42, 25)	5		8	Exp (42, 25)	1
A	Exp (18, 6)	4		E	Exp (18, 6)	Infinitec
B	Exp (18, 6)	4		F	Exp (18, 6) per cycle	1
C	Exp (18, 6)	3		G	Exp (18, 6)	Infinitec
D	Exp (18, 6)e	Infinite		H	Exp (18, 6)e	Infinite
V	Exp (24, 10)	Infinitec		X	Exp (24, 10)	Infinitec
W	Exp (24, 10)	c		21 (Eye Motor)	Saccade and Fixation Timed	1
Y	Exp (24, 10)	2		22 (Mouth)	As a function of number of syllables (Voice key closure time: 100 ms, Wu & Liu, 2008a)	1
Z	Exp (24, 10)	2		23 (Right Hand & Right Arm)	Arm and hand movement time, see Fitts's Law; Finger movement time, see (Wu & Liu, 2008b)	1 (If one movement per time)
25 (Right Foot)	Foot movement time, see (Zhang, Wu, & Wan, 2016; Zhao & Wu, 2013; Zhao, Wu, & Qiao, 2013)	1 (If one movement per time)		24 (Left Hand & Left Arm)	Arm and hand movement time, see Fitts's Law; Finger movement time, see (Wu & Liu, 2008b)	1 (If one movement per time)
26 (Left Foot)	Foot movement time, see (Zhang et al., 2016; Zhao & Wu, 2013; Zhao et al., 2013)	1 (If one movement per time)		27 (Head), 28 (Body), etc.	Head, body movement time etc.c	1 (If one movement per time)

a.处理速度和处理能力是根据人的加工计算模型设定的（Card，et al.，1983）、Wu et al（2008-2017）和Jacobson（1999）

b.实体被定义为给定任务中最小的信息处理单元。例如，在打字任务中，一个字母是一个实体。在语音警告响应任务中，每个短单词都可以视为一个实体。对于语音警告中的长词，每个音节可以表示为一个实体。

c.需要进一步的建模工作和调查

d.见人的加工计算模型(Card, et al., 1983).

e.还取决于信息检索的级别（例如，熟悉程度和检索时间）

 

 

整个模型的方程

方程组EN-1：NASA-TLX测量的工作负荷建模：方程式(10-12)(Wu & Liu, 2007)

 

 

 

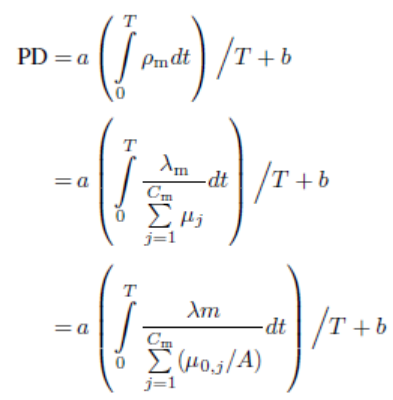
Variables
PD	Physical Demand	How much physical activity was required? Was the task easy or demanding, slack or strenuous?
TD	Temporal Demand	How much time pressure did you feel due to the pace at which the tasks or task elements occurred? Was the pace slow or rapid?
EF	Effort	How hard did you have to work (mentally and physically) to accomplish your level of performance?
PE	Performance	How successful were you in performing the task? How satisfied were you with your performance?
FR	Frustration	How irritated, stressed, and annoyed versus content, relaxed, and complacent did you feel during the task?
MD	Mental Demand	How much mental and perceptual activity was required? Was the task easy or demanding, simple or complex?
A	A factor of aging (A ≥ 1)	The value of A is directly proportional to age, set based on literature
	Arrival rate	The arrival rate of the subnetwork i
	Original processing speed	The original processing speed of server j for the young adults in QN-MHP
	Number of servers	The total number of servers in the subnetwork m
T	Total time of a trial	The total task time of each trial
a	Constant	The constants in representing the direct proportional relation between the averaged utilizations and the subjective responses (a > 0), see the published work
b	Constant	Same above

 

方程组EN-2：以P300波幅和潜伏期衡量的工作负荷建模：方程式(10-11)(Wu, Liu, & Quinn-Walsh, 2008)

 

 

Variables
	Amplitude of the ERP potential P300
Li	Latency of the P300
k	Constant	A constant in this relationship I = kN.
b	Constant	A constant in this inverse relationship
NE	Amount of NE	Modeling NE (norepinephrine) in Synaptic Transmission
	Number	Number of information entities
	Number	Number of information entities of other tasks concurrently processed in server j
	Number	Number of processing cycles for each of those entities at server j
	A random factor	Normally distributed random factor with mean being equal to zero
r	Distance	Distance from the electrical field point (the location where NE is released) to locations of the electrodes on the scalp
	Processing times	Processing times of task i at the perceptual subnetwork, at Server A or B, and at Servers C and E, respectively

 

方程组EN-3：在fMRI建模中的Bold信号：方程式(27)(Wu & Liu, 2008a)

 

 

Variables
CB(t)	The integrated BOLD signal	Modeling of BOLD signal and its percentage of change: The integrated BOLD (blood oxygen level dependent) signal
s	Latency scale
M	Magnitude scale
k,a,b	Parameters	k, a, and b come from the equations of Cohen (1997) and Anderson et al. (2003), determined by the properties of the brain regions with certain fMRI measurement techniques
t	The duration of each trial	Modeling of BOLD Signal and Its Percentage of Change
	The length of time being occupied at a server	In queuing networks can be quantified by Equation 28 (Gross & Harris, 1998):

 

方程组EN-4：基于强化学习算法的实体路线选择和技能获取：方程式(9.7-9.8)(Wu, Berman, & Liu, 2010)

 

Variables
	Processing speed of server i
	The minimal of processing time of server i after intensive practice
	The change of expected value of processing time of server i from the beginning to the end of the practice
	Learning rate of server i
	Number of entities processed by server i

 

 

Variables
	Online Q value	is the online Q value if entity routes from server i to server j in t+1th transition
	Maximum Q value	Maximum Q value routing from server j to next k server(s)
	Processing speed	is the reward and is the processing speed of the server j if entity enters it at tth transition
	Discount parameter	The discount parameter of routing to the next server()
	Learning rate	The learning rate of Q online learning()

 

方程组EN-5：学习过程中的信息处理速度及其变异性变化：方程式(6)(Wu & Liu, 2008b)

 

Variables
X	Summation of processing time of servers (Y)
Yi	Processing time of server i
k	Number of servers in the route
	Arrival rates of entities/information

 

方程组EN-6：将期望效用建模为时间压力下的工作负荷。方程式(2)(Cao & Liu, 2015)

 

Variables
a,b	Parameter	Parameters a and b are the constants in representing the direct proportional relation between the averaged utilizations and the subjective responses (a > 0)
	The average utilization of motor subnetwork	The score of PD reflects workload at the motor component, and therefore, it is in direct proportion to the average utilization of motor subnetwork

 

方程组EN-7：对语音告警的响应时间进行建模。方程式(11，12，13) (Zhang, Wu & Wan, 2016)

Variables	Description
Tk	Notation of processing time of the stimulus at Server k (k =1-8, A,B,C,F,H, W−Z)
T6(0)and T8(0)	The initial entity processing time in Server 6 and Server 8, respectively
UL	The perceived urgency as a function of warning loudness
US	The perceived urgency as a function of signal world choice
pi	Notation of probability of a warning stimulus traveling through a route i (i=I or II)

 

感知子网络

－视觉感知子网络:

服务器1.方程组VP-1：文本信息感知中的眼动建模：方程式(12)(Wu & Liu, 2008b)

 

Variables		Sources
E(FC)	The expected position of the first character in each chunk	Calculation of the Expected Position of the First Character i
E(FP)	The expected position of the fixation point
	The half-range of each chunk under extensive practice condition

 

服务器1.方程组VP-2：图片信息感知中的眼动建模：方程式(3) (Lim & Liu, 2009)

 

Variables
	Importance index of function k	The relatively important function can be given a value 1, and a value 0 is given to the other. The importance index of function k can be calculated.
	The importance value for function k	The importance value for function k obtained from each pair-wise comparisons, either 1 or 0.

 

服务器3.方程组VP-3：视觉光流感知和速度感知：方程（1）(Zhao & Wu, 2013)

 

Variables
	Perceived speed
V	Actual speed
	The current texture density
	The texture density in the last driving scenario
	The eye height in the last driving scenario
	The current eye height
	two constant parameters

 

服务器4.方程组VP-4：具有检测距离和图像矩阵的视觉检测建模：方程式(12)(Bi, Tsimhoni, & Liu, 2009)

 

Variables
RPOT	Square root of the number of pixels on a target
f	Focal length
S	Size of the area of a target object.
D	Distance of the image forming

 

－语音感知子网络:

服务器6.方程组AP-1：模拟响度对语音告警感知的影响：方程式(1，11) (Zhang, Wu, & Wan, 2016)

 

Variables
	The perceived urgency	Modeling the relationship between loudness and perceived urgency
,	Constants	The relationship between intensity and perceived urgency was quantified: = 1.33, = −0.64,
	Random factors	distributed random factors following distribution [0, 0.7]
L	Loudness level

 

 

Variables
	The effect of loudness on reaction time
	The initial entity processing time in Server 6
	The effect of loudness on perceived urgency

 

服务器8.方程组AP-2：信号词对语音预警感知的影响建模：方程(12) (Zhang, Wu, & Wan, 2016)

 

Variables
	The effect of signal word choice on reaction time
	The entity processing time in Server 8
	The urgency level expressed by the initial words
	The number of words in the ith speech warning

 

 

认知子网络

－服务器B:

方程组C-1：文本信息的最优分块建模：方程式(22) (Wu & Liu, 2008b)

 

Variables	Description
Z	Objective function of task completion time
	Overall duration of processing each chunk at servers after server B
N	Total number of entities processed
x	Chunk size
	Rate of retrieval failure at server B
R	Average duration to correct an error caused by a wrongly processed entity or character

 

方程组C-2：语音信息记忆衰减的建模：方程(7) ( Zhang, Wu, & Wan, 2016)

 

Variables	Description
	The probability of memory decay
	Lead time of a speech warning

 

方程组C-3：对语音告警的强化学习中的路径选择概率进行建模：方程式(4-5) ( Zhang, Wu, & Wan, 2016)

 

Variables
	The route choice error rate
	The error rate when a speech warning travels via route i
	The probability of a speech warning entity processed via route i

 

 

Variables
	The error rate of route choice
L	Loudness level in dB
	Perceived urgency level with different signal word choice
,	Parameters to quantify the power law of perceived urgency and loudness
,	Parameters to quantify the power law of perceived annoyance and loudness
pI, pII	Probabilities of choosing route I (the shorter route) and route II (the longer route)

 

－服务器C:

方程组C-4：抑制不相容反应建模：方程式(4-6) (Wu & Liu, 2008a)

 

Variables
T2,C-comp and T2,F-comp,	Processing times of Server C and F in the compatible conditions
T2,C-incomp and T2,F-incomp	Processing times of Server C and F in the incompatible conditions
SOA (stimulus onset asynchrony)	The delay between the presentation of the stimuli of T1 and T2
Tk	Processing time at server k (k=AP, VP, A, B, C, F, W, Y, Z, X)

 

方程组C-5：双重任务干扰建模：方程式(8-9) (Lin & Wu, 2012)

 

 

Variables	Description	Sources
DLi	Delay time
Ti,C	The entity processing time needed at Server C
PTi-1	Time lapse for the previous key to be pressed
Iv	Inter stimulus interval
Iv + TAP+ TB	Time lapse for the entity of the on-going stimulus to leave Server B
PTi-1-(Iv +TAP+TB)	The least duration that the current stimulus needs to wait at Server C
TC	Cycle time at Server C

 

－服务器E:

方程组C-6：动作控制中的背景噪声：方程式(15) (Lin & Wu, 2012)

 

Variables
	The extent of SDN added with muscle activation level u;	Modelling baseline errors in numerical typing
,	Experimental constants	Modelling baseline errors in numerical typing
u	Muscle activation level	Modelling baseline errors in numerical typing
c	The extent of temporal noise	c is the extent of TN which accumulates as movement time increases
I	Interference index	I was an interference index accounting for the relative extent of the dual-task interference in background noise (CN).

 

－服务器 F

方程组C-7：多任务中的选择反应建模：方程式(B16) (Wu & Liu, 2008a)

 

 

Variables
E(RT2)	Expected reaction time
SOA	Stimulus-onset asynchrony	The time difference between the onset of the two stimuli from two tasks
Ti	Processing time of servers see (Wu & Liu, 2008a)
TFst

 

方程组C-8：建模响应复杂度的影响（同时使用一个手指或多个手指）：公式（1-13）(Lin & Wu, 2012)

 

Variables
	Response time to i th stimulus with a finger strategy under an urgency condition
	Finger strategy
i	Response order
T	Processing time

 

方程组C-9：具有值矩阵的复杂决策：公式（5）(Zhao & Wu, 2013)

 

Variables
P(t)	Speed choice at time t
V(t)	Momentary valence
M(n)	Human subjective attribute matrix
W(t)	Attention weight matrix
S	Feedback matrix

 

方程组C-10：感知风险建模：方程式(5) (Zhuang & Wu, 2013)

 

Variables
PRv	Human perceived risk increases with higher risk from vehicles
PRl	Human perceived risk increases with higher risk from local-defined risk
ag	A coefficient adjusting effect of group size of human
Ngroup	Group size of human

 

方程组C-11：横向控制决策：方程式（1，2） (Bi, Gan, Shang, & Liu, 2012)

 

 

Variables
	Increment of steering angle
kp, kd	The coefficients of proportional derivative controller
a'y	The first derivative of acceleration
E	Error between the desired lateral position gained with the predefined desired path and predictive lateral position computed with the internal vehicle dynamics model
v	Current lateral velocity
tp	Preview time

 

方程组C-12：对风险评估的准确性建模：方程式（8，16，21）( Zhang, Wu, & Wan, 2016)

 

 

 

Variables
	The effect of hazard evaluation accuracy on error rate
	Perceived value of hazard
	Actual value of hazard
	Estimated distance
	Threshold of perceived distance
	Actual distance between the current position of warning receiving vehicle
v(t)	Instant speed	The instant speed (v) and acceleration (at) at time t is modeled in [23] as follows:
	Global optic flow rate of the textured ground surface	φ is the global optic flow rate of the textured ground surface, a proportion of speed as long as eye height is constant
k	Parameter	The parameter k is quantified by the annual mileage divided by a maximum value of annual mileage in general
	Perceived time-to-collision	The perceived time-to-collision (TTCp) will be affected by the existence of the lead vehicle. TTC is the actual time to collision that the vehicle will be able to avoid a collision without exceeding the assumed maximum deceleration
LV	Lead vehicle status	LV is a dichotomous variable of the lead vehicle in order to model the effect of the lead vehicle on TTCp (0 = without lead vehicle; 1 = with lead vehicle)
	Lead time of speech warning

 

－服务器G:

方程组C-13：紧迫性和动机建模：方程式(12) (Lin & Wu, 2012)

 

Variables
	Response time to i th stimulus with a finger strategy under an urgency condition
RT	Reaction time
DL	Delay time caused by dual-task interference
MT	Movement time
	Key-closure Time
	Finger strategy	notation of finger strategy. =0 →Single finger typing; =1 →Multi-finger typing
	Urgency	notation of urgency. =1→non-urgent condition; =0→urgent condition
i	Response order	notation of response order. i=1→first response in 9-digit number, and so on.

 

动作控制子网络

－服务器W:

方程组M-1：学习过程中的运动程序检索建模：方程式(2) (Wu & Liu, 2008b)

 

Variables
	Processing time in each server	Reduction of Server Processing Time.
	Expected minimal processing time (Ti) at server i after intensive practice	Feyen (2002)
	Change in the expected processing time from the beginning to the end of practice	Reduction of Server Processing Time.
	Learning rate of server i	Heathcote et al. (2000)
	Number of entities processed by server i	Reduction of Server Processing Time.

 

－服务器X:

方程组M-2：闭环动作控制中的误差校正模型：方程式（24-32）(Lin & Wu, 2012)

 

 

Variables
	The uncorrected portion of endpoint variability	Endpoint variability in different conditions
MT	Movement time	Modelling response time of numerical typing: the general equation of response time
DL	Delay time caused by dual-task interference	Modelling response time of numerical typing: the general equation of response time
Err%	Estimations of error rates	Estimations of error rates (Err%) in jth typing conditions
P(), P()	Parameters	The probability of errors in X-direction and Y-direction during jth experimental condition

 

－手服务器（服务器23，24）:

方程组M-3：QWERTY键盘输入中手和手指移动的时间和错误：方程式(19) (Wu & Liu, 2008b)

 

Variables
Dis	Movement distance	Distribution of Movement Distance.
M	Population size	Equation (19) can be used to estimate the distribution of movement distance of different body parts including hands and fingers.
RD	Movement radius	Equation (19) can be used to estimate the distribution of movement distance of different body parts including hands and fingers.

 

方程组M-4：双手（两只手）配合：方程（31-34）(Wu & Liu, 2008b)

 

 

 

 

Variables
Y	Time	The time (Y) saved by optimization of EPD
EPD	Error Prevention Duration	The optimization process of EPD is a trade-off between the time in typing and the time in error correcting
N	Number	The number of characters typed
	Parameter	It specifies how long to correct one transposition error
e	Parameter	It refers to the error rate of the transposition error made by reducing of EPD

 

方程组M-5：数字打字中的手和手指移动时间和错误：方程式(13)(16) (Lin & Wu, 2012)

 

Variables
	Response time to ith stimulus with a finger strategy under β urgency condition	Modelling response time of numerical typing: the general equation of response time
	The processing time of ith stimulus at Server k	All Tk are estimated based on parameter settings in QN-MHP
D	Travel distance	Modelling baseline response time in numerical typing
	Effective target size	The effective target size (Se) is calculated based on the maximal target width that can be utilized without touching adjacent keys:
	Constant	Im =100 is used as it was suggested in the original study (Card et al. 1983)
	Key-closure Time	Modelling response time of numerical typing: the general equation of response time

 

 

Variables	Description
	The Extent of SDN added with muscle activation level u in theexperimental condition
	Muscle activation level in theexperimental condition
	Extent of TN in theexperimental condition
	Interference index
,	Experimental constants

 

－脚服务器（服务器25）

方程组M-6：脚踩踏板时的运动时间：方程式(21) (Wu & Liu, 2008b)

 

Variables	Description	Sources
MT	Movement time	The foot server executes the simulated movement to press a pedal and its movement time () can be estimated by the formula proposed by Drury[1975]
S	Shoe width	S refers to the shoe width [10cm, Armstrong 2004]
W	Pedal width	W is the pedal width (10cm, same with the shoe width)
A	Parameter	A stands for the movement distance (3cm, typical movement distance for a foot pedal).

 

方程组M-7：不考虑人的个性作为个体差异因素的脚部运动的角速度：方程式(3) (Zhao, Wu, & Qiao, 2013)

 

Variables	Description	Sources
	Pedal angular velocity	Mathematical Model of Human operator Speed Control: Speed Adjustment
A	Constant	Mathematical Model of Human operator Speed Control: Speed Adjustment
	Target speed	Mathematical Model of Human operator Speed Control: Speed Adjustment
	Perceived speed	Mathematical Model of Human operator Speed Control: Speed Adjustment

 

方程组M-8：考虑人的个性作为个体差异因素的脚部运动的角速度 (Zhao & Wu, 2013)(Zhao & Wu, 2013)

 

Variables	Description
	Pedal angular velocity
A	Constant
	Target speed
	Perceived speed
η	Personality index

 

 

方程组M-9：人的目标速度对车辆运动速度的影响：方程（6）(Zhao & Wu, 2013)

 

Variables	Description	Sources
V	Vehicle speed	Mathematical Model of Human operator Speed Control: Vehicle Mechanics
	Vehicle acceleration	Mathematical Model of Human operator Speed Control: Vehicle Mechanics
vtar	Target speed of a human operator
	Initial acceleration	Mathematical Model of Human operator Speed Control: Vehicle Mechanics
	Coefficient of the overall drag on the vehicle	Mathematical Model of Human operator Speed Control: Vehicle Mechanics
A,B	Constants	Mathematical Model of Driver Speed Control: Vehicle Mechanics

 

 

5. 使用QN-MHP对人的绩效进行数学建模的主要贡献者（欢迎加入我们！Email:changxuwu@gmail.com）

我们特别感谢密歇根大学的Dr. Yili Liu，他用排队网络理论统一了现有的反应时间模型，为人的绩效的排队网络建模奠定了理论基础。

Dr. Changxu Wu (Group Coordinator) at University of Arizona, USA

Dr. Robert Feyen, University of Minnesota, USA

Dr. Omer Tsimhoni, General Motors, USA

Dr. Ji Hyoun Lim, Apple, USA; Hongik University, Korea

Dr. Luzheng Bi at Beijing Institute of Technology, China

Dr. Shi Cao at University of Waterloo, Canada

Dr. Guozhen Zhao at Chinese Academy of Sciences, China

Dr. Cheng-Jhe (Robert) Lin, National Taiwan University of Science and Technology

Dr. Jingyan Wan, General Motors, USA

Dr. Yiqi Zhang at Pen State University, USA

 

 

6. 发表QN-MHP模型文章的国内外科研机构

美国密歇根大学

美国杜克大学

美国宾夕法尼亚州立大学

美国纽约州立大学

美国亚利桑那大学

美国密歇根理工大学

韩国首尔大学

清华大学

中国科学院

台湾清华大学

北京理工大学

四川大学

 

7. 已经运用QN-MHP模型作为主要建模方法的国际期刊和会议文章

 Bi, L. Z., Gan, G. D., Shang, J. X., & Liu, Y. L. (2012). Queuing Network Modeling of Driver Lateral Control With or Without a Cognitive Distraction Task [Article]. Ieee Transactions on Intelligent Transportation Systems, 13(4), 1810-1820. https://doi.org/10.1109/Tits.2012.2204255

Bi, L. Z., Tsimhoni, O., & Liu, Y. L. (2009). Using Image-Based Metrics to Model Pedestrian Detection Performance With Night-Vision Systems [Article]. Ieee Transactions on Intelligent Transportation Systems, 10(1), 155-164. https://doi.org/10.1109/Tits.2008.2011719

Bi, L. Z., Wang, M. T., Wang, C. E., & Liu, Y. L. (2015). Development of a Driver Lateral Control Model by Integrating Neuromuscular Dynamics Into the Queuing Network-Based Driver Model [Article]. Ieee Transactions on Intelligent Transportation Systems, 16(5), 2479-2486. https://doi.org/10.1109/Tits.2015.2409115

Cao, S., & Liu, Y. (2015). Modelling workload in cognitive and concurrent tasks with time stress using an integrated cognitive architecture. International Journal of Human Factors Modelling and Simulation, 5(2), 113-135. https://doi.org/10.1504/ijhfms.2015.075360

Chikodili, H. U., Mathew, C. O., & Caroline, N. A. (2017). Performance evaluation of law enforcement agency on crime information management using queuing network model. International Journal of Physical Sciences, 12(4), 38-51. https://doi.org/10.5897/ijps2016.4581

Feng, F., Liu, Y., Chen, Y., Filev, D., & To, C. (2014). Computer-aided usability evaluation of in-vehicle infotainment systems. Proceedings of the Human Factors and Ergonomics Society Annual Meeting,

Feng, F., Liu, Y. L., & Chen, Y. F. (2017). A computer-aided usability testing tool for in-vehicle infotainment systems [Article]. Computers & Industrial Engineering, 109, 313-324. https://doi.org/10.1016/j.cie.2017.05.019

Fu, X. L., Cai, L. H., Liu, Y., Jia, J., Chen, W. F., Yi, Z., Zhao, G. Z., Liu, Y. J., & Wu, C. X. (2014). A computational cognition model of perception, memory, and judgment [Article]. Science China-Information Sciences, 57(3), 15, Article 032114. https://doi.org/10.1007/s11432-013-4911-9

Fuller, H. J., Reed, M. P., & Liu, Y. (2010). Integrating physical and cognitive human models to represent driving behavior. Proceedings of the Human Factors and Ergonomics Society Annual Meeting,

Fuller, H. J. A., Reed, M. P., & Liu, Y. L. (2012). Integration of Physical and Cognitive Human Models to Simulate Driving With a Secondary In-Vehicle Task [Article]. Ieee Transactions on Intelligent Transportation Systems, 13(2), 967-972. https://doi.org/10.1109/Tits.2012.2182764

Gil, G. H., & Kaber, D. B. (2012). An Accessible Cognitive Modeling Tool for Evaluation of Pilot-Automation Interaction [Article]. International Journal of Aviation Psychology, 22(4), 319-342. https://doi.org/10.1080/10508414.2012.718236

Jeong, H., & Liu, Y. (2016). Computational Modeling of Finger Swipe Gestures on Touchscreen: Application of Fitts’ Law in 3D Space. Proceedings of the Human Factors and Ergonomics Society Annual Meeting,

Jeong, H., & Liu, Y. L. (2019). Computational Modeling of Touchscreen Drag Gestures Using a Cognitive Architecture and Motion Tracking [Article]. International Journal of Human-Computer Interaction, 35(6), 510-520. https://doi.org/10.1080/10447318.2018.1466858

Ko, S., Kutchek, K., Zhang, Y., & Jeon, M. (2021). Effects of Non-Speech Auditory Cues on Control Transition Behaviors in Semi-Automated Vehicles: Empirical Study, Modeling, and Validation [Article]. International Journal of Human–Computer Interaction, 38(2), 185-200. https://doi.org/10.1080/10447318.2021.1937876

Li, H., Bi, L., & Shi, H. (2020). Modeling of Human Operator Behavior for Brain-Actuated Mobile Robots Steering [Article]. IEEE Trans Neural Syst Rehabil Eng, 28(9), 2063-2072. https://doi.org/10.1109/TNSRE.2020.3009376

Lim, J. H., & Liu, Y. (2004). A queuing network model for visual search and menu selection. Proceedings of the Human Factors and Ergonomics Society Annual Meeting,

Lim, J. H., & Liu, Y. L. (2009). Modeling the Influences of Cyclic Top-Down and Bottom-Up Processes for Reinforcement Learning in Eye Movements [Article]. Ieee Transactions on Systems Man and Cybernetics Part a-Systems and Humans, 39(4), 706-714. https://doi.org/10.1109/Tsmca.2009.2018635

Lim, J. H., Liu, Y. L., & Tsimhoni, O. (2010). Investigation of Driver Performance With Night-Vision and Pedestrian-Detection Systems-Part 2: Queuing Network Human Performance Modeling [Article]. Ieee Transactions on Intelligent Transportation Systems, 11(4), 765-772. https://doi.org/10.1109/Tits.2010.2049844

Lin, B. T. W., & Hwang, S. L. (2012). Effect prediction of time-gaps for adaptive cruise control (ACC) and in-vehicle tasks on bus driver performance [Article]. Safety Science, 50(1), 68-75. https://doi.org/10.1016/j.ssci.2011.07.003

Lin, C.-J., Wu, C., & Chaovalitwongsec, W. A. (2014). Integrating behavior modeling with data mining to improve human error prediction in numerical data entry. Proceedings of the human factors and ergonomics society annual meeting,

Lin, C. J., & Wu, C. (2012). Mathematically modelling the effects of pacing, finger strategies and urgency on numerical typing performance with queuing network model human processor [Article]. Ergonomics, 55(10), 1180-1204. https://doi.org/10.1080/00140139.2012.697583

Lin, C. J., Wu, C. X., & Chaovalitwongse, W. A. (2015). Integrating Human Behavior Modeling and Data Mining Techniques to Predict Human Errors in Numerical Typing [Article]. Ieee Transactions on Human-Machine Systems, 45(1), 39-50. https://doi.org/10.1109/Thms.2014.2357178

Liu, Y., Feyen, R., & Tsimhoni, O. (2006). Queueing Network-Model Human Processor (QN-MHP). Acm Transactions on Computer-Human Interaction, 13(1), 37-70. https://doi.org/10.1145/1143518.1143520

Liu, Y., & Wu, C. (2006). Modeling Percentage Change of fMRI BOLD Signal and Reaction Time of a Dual Task with a Queuing Network Modeling Approach. Proceedings of the Annual Meeting of the Cognitive Science Society,

Liu, Y., Wu, C., & Berman, M. G. (2012). Computational neuroergonomics [Article]. Neuroimage, 59(1), 109-116. https://doi.org/10.1016/j.neuroimage.2011.05.027

Liu, Y. L. (2009). QN-ACES: Integrating Queueing Network and ACT-R, CAPS, EPIC, and Soar Architectures for Multitask Cognitive Modeling [Article]. International Journal of Human-Computer Interaction, 25(6), 554-581, Article Pii 913657582. https://doi.org/10.1080/10447310902973182

Rhie, Y. L., Lim, J. H., & Yun, M. H. (2019). Queueing Network Based Driver Model for Varying Levels of Information Processing [Article]. Ieee Transactions on Human-Machine Systems, 49(6), 508-517. https://doi.org/10.1109/Thms.2018.2874183

Tsimhoni, O., & Liu, Y. (2003). Modeling steering using the queueing network—model human processor (QN-MHP). Proceedings of the human factors and ergonomics society annual meeting,

Tsimhoni, O., & Reed, M. P. (2007). The virtual driver: Integrating task planning and cognitive simulation with human movement models. SAE Transactions, 1525-1531. https://doi.org/10.4271/2007-01-1766

Wu, C. (2018). The Five Key Questions of Human Performance Modeling [Article]. Int J Ind Ergon, 63, 3-6. https://doi.org/10.1016/j.ergon.2016.05.007

Wu, C., & Liu, Y. (2004). Modeling human transcription typing with queuing network-model human processor (QN-MHP). Proceedings of the human factors and ergonomics society annual meeting,

Wu, C., & Liu, Y. (2006). Queuing network modeling of age differences in driver mental workload and performance. Proceedings of the Human Factors and Ergonomics Society Annual Meeting,

Wu, C., & Liu, Y. (2008a). Queuing network modeling of the psychological refractory period (PRP). Psychol Rev, 115(4), 913-954. https://doi.org/10.1037/a0013123

Wu, C., & Liu, Y. (2008b). Queuing network modeling of transcription typing [Review]. Acm Transactions on Computer-Human Interaction, 15(1), 45. https://doi.org/10.1145/1352782.1352788

Wu, C. X., Liu, Y. J., & Lin, B. (2012). A Queueing Model Based Intelligent Human-Machine Task Allocator [Article]. Ieee Transactions on Intelligent Transportation Systems, 13(3), 1125-1137. https://doi.org/10.1109/Tits.2012.2187351

Wu, C. X., & Liu, Y. L. (2007a). Queuing network modeling of driver workload and performance [Article]. Ieee Transactions on Intelligent Transportation Systems, 8(3), 528-537. https://doi.org/10.1109/Tits.2007.903443

Wu, C. X., & Liu, Y. L. (2007b). Usability Makeover of a Cognitive Modeling Tool [Editorial Material]. Ergonomics in Design, 15(2), 8-14. https://doi.org/Doi 10.1177/106480460701500201

Wu, C. X., & Liu, Y. L. (2009). Development and evaluation of an ergonomic software package for predicting multiple-task human performance and mental workload in human-machine interface design and evaluation [Article]. Computers & Industrial Engineering, 56(1), 323-333. https://doi.org/10.1016/j.cie.2008.06.013

Wu, C. X., Liu, Y. L., & Quinn-Walsh, C. M. (2008). Queuing network modeling of a real-time psychophysiological index of mental workload - P300 in event-related potential (ERP) [Article]. Ieee Transactions on Systems Man and Cybernetics Part a-Systems and Humans, 38(5), 1068-1084. https://doi.org/10.1109/Tsmca.2008.2001070

Wu, C. X., Tsimhoni, O., & Liu, Y. L. (2008). Development of an adaptive workload management system using the queueing network-model human processor (QN-MHP) [Article]. Ieee Transactions on Intelligent Transportation Systems, 9(3), 463-475. https://doi.org/10.1109/Tits.2008.928172

Zhang, Y., & Wu, C. (2014). Modeling the effect of loudness and semantics of speech warnings on human performances. Proceedings of the Human Factors and Ergonomics Society Annual Meeting,

Zhang, Y., & Wu, C. (2017). Learn to integrate mathematical models in human performance modeling. Proceedings of the Human Factors and Ergonomics Society Annual Meeting,

Zhang, Y. Q., Wu, C. X., Qiao, C. M., Sadek, A., & Hulme, K. F. (2022). A Cognitive Computational Model of Driver Warning Response Performance in Connected Vehicle Systems [Article; Early Access]. Ieee Transactions on Intelligent Transportation Systems, 16. https://doi.org/10.1109/Tits.2021.3134058

Zhang, Y. Q., Wu, C. X., & Wan, J. Y. (2016). Mathematical Modeling of the Effects of Speech Warning Characteristics on Human Performance and Its Application in Transportation Cyberphysical Systems [Article]. Ieee Transactions on Intelligent Transportation Systems, 17(11), 3062-3074. https://doi.org/10.1109/Tits.2016.2539975

Zhang, Y. Q., Wu, C. X., & Wan, J. Y. (2017). A human-in-the-loop wireless warning message notification model and its application in connected vehicle systems [Article]. Journal of Intelligent Transportation Systems, 21(2), 148-166. https://doi.org/10.1080/15472450.2016.1254045

Zhao, G., Wu, C., & Ou, B. (2011). Mathematical modeling of average driver speed control with the integration of queuing network-model human processor and rule-based decision field theory. Proceedings of the Human Factors and Ergonomics Society Annual Meeting,

Zhao, G. Z., & Wu, C. X. (2013). Mathematical Modeling of Driver Speed Control With Individual Differences [Article]. Ieee Transactions on Systems Man Cybernetics-Systems, 43(5), 1091-1104. https://doi.org/10.1109/Tsmc.2013.2256854

Zhao, G. Z., Wu, C. X., & Qiao, C. M. (2013). A Mathematical Model for the Prediction of Speeding with its Validation [Article]. Ieee Transactions on Intelligent Transportation Systems, 14(2), 828-836. https://doi.org/10.1109/Tits.2013.2257757

Zhuang, X. L., & Wu, C. X. (2013). Modeling Pedestrian Crossing Paths at Unmarked Roadways [Article]. Ieee Transactions on Intelligent Transportation Systems, 14(3), 1438-1448. https://doi.org/10.1109/Tits.2013.2267734

若要成为人类绩效建模中数学建模小组的成员（用户或贡献者），请发送电子邮件至changxu.wu@gmailcom（请列出您的全名和机构/公司名称），我们将向您发送最新更新，新的建模工作，和新教程。所有这些都是免费的。