Mathematical Modeling of Human Performance and Cognition

[Features]

[Framework & Equations]

[Tutorials & Membership]

[Contributors & Users]

[Design Tools]

The goal of this document is to summarize and integrate all mathematical modeling work that quantifies the different aspects and components of human cognition and performance. It will also serve as a learning material platform for new users of mathematical modeling of human performance.

1. Unique Features of Mathematical Modeling of Human Performance and Cognition

Mathematical equations can predict, quantify and analyze human performance, workload, brain waves, and other indexes of human behavior in a rigorous way. Compared with computer simulation,

1) Mathematical models and equations of human behavior clearly quantify and extract the mechanisms of human behavior by clear quantifications of the relationships of variables including the relationship between the input and output of each equation. Users of these mathematical models will be much easier to understand and extract the relationships among variables than reading computer codes.

2) Mathematical models and equations of human behavior can be relatively easily to be edited, modified, improved, and integrated together to develop new mathematical equations.

3) Mathematical models and equations of human behavior and performance can be relatively easily be implemented in different programming languages and be imbedded in different intelligent systems to work together with system design.

4) Mathematical models and equations can lead to analytical solutions, which are more accurate than simulation results.

5) There are mathematical models and equations quantifying the entire human cognition system (See equations in the entire network) which is another unique feature of the mathematical modeling approach.

6) There are mathematical models and equations can be proved by mathematics derivation directly with no need to be verified by empirical data (See Equations in Wu, C., Berman, M., & Liu, Y., 2010).

2. Usage of Mathematical Models and Equations in this Summary Webpage

The equations summarized here can also serve as an index page and a guideline tool for modelers who can:

1) Use those mathematical models to quantify and predict new phenomena and tasks in human performance

2) Add and develop new equations and mathematical models to quantify new components of human cognition and performance to further grow with the framework of the Queuing Network-Model Human Processor (QN-MHP)

3) To be used and imbedded in different intelligent systems and tool design for human performance and behavior predictions

Tutorial and Free Membership:

1) How to build and verify models of human performance (General Descriptions) (Wu, 2016) and YouTube Video

2) How to build mathematical models (e.g., Page 9-10) (Wu & Liu, 2008a): Free tutorial video please email Dr.Wu changxu.wu@gmail.com

3) How to integrate and build new mathematical models in human performance modeling (Zhang & Wu, 2017)

4) To become a member (user or contributor) of mathematical modeling group in human performance modeling, please email to changxu.wu@gmailcom (Please list your full name and institution/company name), we will send you recent updates, new modeling work, and new tutorials. All of them are free.

3. Human Machine System Design Tools based on the Equations on this Page [Link]

4. Mathematical Equations in the Queuing Network-Model Human Processors (QN-MHP) as the Framework

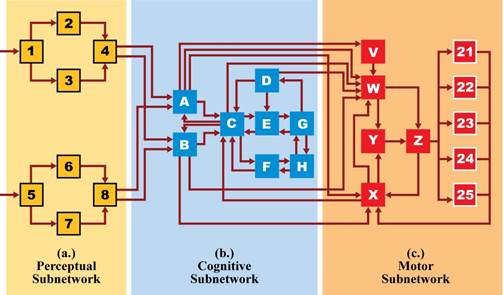
The General Structure of Queuing Network-Model Human Processor (QN-MHP)

(a.) Perceptual Subnetwork	(b.) Cognitive Subnetwork	(c.) Motor Subnetwork
1. Common visual processing 2. Visual recognition 3. Visual location 4. Visual recognition and location integration 5. Common auditory processing 6. Auditory recognition 7. Auditory location 8. Auditory recognition and location integration	A. Visuospatial sketchpad B. Phonological loop C. Central executive D. Long-term procedural memory E. Performance monitor F. Complex cognitive function G. Goal initiation H. Long-term declarative & spatial memory	V. Sensorimotor integration W. Motor program retrieval X. Feedback information collection Y. Motor program assembling and error detecting Z. Sending information to body parts 21-25 etc.: Body parts: eye, mouth, left hand, right hand, foot

Server Information Processing Time and Information Processing Capacities

Server Name	Processing Time^a: Exponential Distribution (Mean, Min) (ms)	Capacity (Entities^a)	Server Name	Processing Time: Exponential Distribution (Mean, Min) (ms)	Capacity (Entities^b)
1	Exp (42, 25)	4	5	Exp (42, 25)	2
2	Exp (42, 25)	4	6	Exp (42, 25)	1
3	Exp (42, 25)	4	7	Exp (42, 25)	1
4	Exp (42, 25)	5	8	Exp (42, 25)	1
A	Exp (18, 6)	4	E	Exp (18, 6)	Infinite^c
B	Exp (18, 6)	4	F	Exp (18, 6) per cycle	1
C	Exp (18, 6)	3	G	Exp (18, 6)	Infinite^c
D	Exp (18, 6)^e	Infinite	H	Exp (18, 6)^e	Infinite
V	Exp (24, 10)	Infinite^c	X	Exp (24, 10)	Infinite^c
W	Exp (24, 10)	1^c	21 (Eye Motor)	Saccade and Fixation Time^d	1
Y	Exp (24, 10)	2	22 (Mouth)	As a function of number of syllables (Voice key closure time: 100 ms, Wu & Liu, 2008a)	1
Z	Exp (24, 10)	2	23 (Right Hand & Right Arm)	Arm and hand movement time, see Fitts's Law; Finger movement time, see (Wu & Liu, 2008b)	1 (If one movement per time)
25 (Right Foot)	Foot movement time, see (Zhang, Wu, & Wan, 2016; Zhao & Wu, 2013; Zhao, Wu, & Qiao, 2013)	1 (If one movement per time)	24 (Left Hand & Left Arm)	Arm and hand movement time, see Fitts's Law; Finger movement time, see (Wu & Liu, 2008b)	1 (If one movement per time)
26 (Left Foot)	Foot movement time, see (Zhang et al., 2016; Zhao & Wu, 2013; Zhao et al., 2013)	1 (If one movement per time)	27 (Head), 28 (Body), etc.	Head, body movement time etc.^c	1 (If one movement per time)

a. Processing speed and capacities were set based on Model Human Processor (Card, et al., 1983), Wu et al (2008-2017), and Jacobson (1999).

b. Entity is defined as the smallest information processing unit in a given task. For example, in a typing task, one letter is an entity. In a speech warning responding task, each short word can be regarded as one entity. For long words in speech warning, each syllable can be represented as one entity.

c. Needs further modeling work and investigation.

d. See Model Human Processor (Card, et al., 1983).

e. Also depends on level of information retrieval (e.g., familiarity and number of time of retrieval).

Entire Network

Equation Set EN-1: Mental workload modeling measured by NASA-TLX: Equation (10-12) (Wu & Liu, 2007)

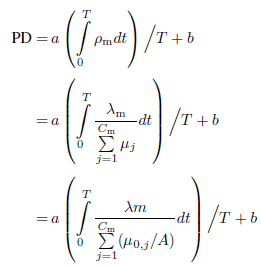
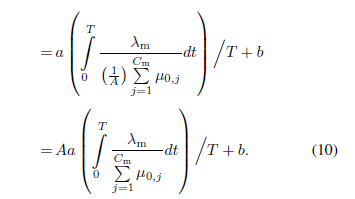
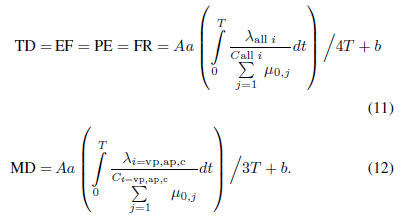
Variables
PD	Physical Demand	How much physical activity was required? Was the task easy or demanding, slack or strenuous?
TD	Temporal Demand	How much time pressure did you feel due to the pace at which the tasks or task elements occurred? Was the pace slow or rapid?
EF	Effort	How hard did you have to work (mentally and physically) to accomplish your level of performance?
PE	Performance	How successful were you in performing the task? How satisfied were you with your performance?
FR	Frustration	How irritated, stressed, and annoyed versus content, relaxed, and complacent did you feel during the task?
MD	Mental Demand	How much mental and perceptual activity was required? Was the task easy or demanding, simple or complex?
A	A factor of aging (A ≥ 1)	The value of A is directly proportional to age, set based on literature
	Arrival rate	The arrival rate of the subnetwork i
	Original processing speed	The original processing speed of server j for the young adults in QN-MHP
	Number of servers	The total number of servers in the subnetwork m
T	Total time of a trial	The total task time of each trial
a	Constant	The constants in representing the direct proportional relation between the averaged utilizations and the subjective responses (a > 0), see the published work
b	Constant	Same above

Equation Set EN-2: Mental workload modeling measured by P300 amplitude and latency: Equation (10-11) (Wu, Liu, & Quinn-Walsh, 2008)

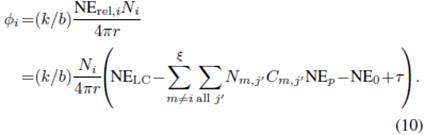
Variables
	Amplitude of the ERP potential P300
Li	Latency of the P300
k	Constant	A constant in this relationship I = kN.
b	Constant	A constant in this inverse relationship
NE	Amount of NE	Modeling NE (norepinephrine) in Synaptic Transmission
	Number	Number of information entities
	Number	Number of information entities of other tasks concurrently processed in server j
	Number	Number of processing cycles for each of those entities at server j
	A random factor	Normally distributed random factor with mean being equal to zero
r	Distance	Distance from the electrical field point (the location where NE is released) to locations of the electrodes on the scalp
	Processing times	Processing times of task i at the perceptual subnetwork, at Server A or B, and at Servers C and E, respectively

Equation Set EN-3: Bold signal in fMRI modeling: Equation (27) (Wu & Liu, 2008a)

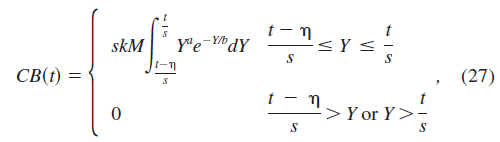
Variables
CB(t)	The integrated BOLD signal	Modeling of BOLD signal and its percentage of change: The integrated BOLD (blood oxygen level dependent) signal
s	Latency scale
M	Magnitude scale
k,a,b	Parameters	k, a, and b come from the equations of Cohen (1997) and Anderson et al. (2003), determined by the properties of the brain regions with certain fMRI measurement techniques
t	The duration of each trial	Modeling of BOLD Signal and Its Percentage of Change
	The length of time being occupied at a server	In queuing networks can be quantified by Equation 28 (Gross & Harris, 1998):

Equation Set EN-4: Entity route selections and skill acquisitions based on reinforcement learning algorithms: Equation (9.7-9.8) (Wu, Berman, & Liu, 2010)

Variables
	Processing speed of server i
	The minimal of processing time of server i after intensive practice
	The change of expected value of processing time of server i from the beginning to the end of the practice
	Learning rate of server i
	Number of entities processed by server i

Variables
	Online Q value	is the online Q value if entity routes from server i to server j in t+1th transition
	Maximum Q value	Maximum Q value routing from server j to next k server(s)
	Processing speed	is the reward and is the processing speed of the server j if entity enters it at tth transition
	Discount parameter	The discount parameter of routing to the next server()
	Learning rate	The learning rate of Q online learning()

Equation Set EN-5: Information processing speed and its variability changes in learning process: Equation (6) (Wu & Liu, 2008b)

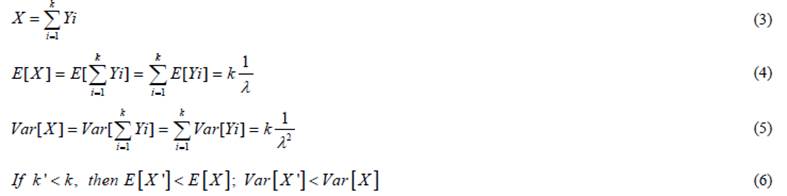
Variables
X	Summation of processing time of servers (Y)
Yi	Processing time of server i
k	Number of servers in the route
	Arrival rates of entities/information

Equation Set EN-6: Modeling the expected utilization as the mental workload under the time stress. Equation (2) (Cao & Liu, 2015)

Variables
a,b	Parameter	Parameters a and b are the constants in representing the direct proportional relation between the averaged utilizations and the subjective responses (a > 0)
	The average utilization of motor subnetwork	The score of PD reflects workload at the motor component, and therefore, it is in direct proportion to the average utilization of motor subnetwork

Equation Set EN-7: Modeling the response time of speech warnings. Equation (11, 12, 13) (Zhang, Wu & Wan, 2016)

Variables	Description
Tk	Notation of processing time of the stimulus at Server k (k =1-8, A,B,C,F,H, W−Z)
T6(0)and T8(0)	The initial entity processing time in Server 6 and Server 8, respectively
UL	The perceived urgency as a function of warning loudness
US	The perceived urgency as a function of signal world choice
pi	Notation of probability of a warning stimulus traveling through a route i (i=I or II)

Perceptual Subnetwork

－Visual perceptual subnetwork:

Server 1. Equation Set VP-1: Eye movement modeling in textual information perception: Equation (12) (Wu & Liu, 2008b)

Variables		Sources
E(FC)	The expected position of the first character in each chunk	Calculation of the Expected Position of the First Character i
E(FP)	The expected position of the fixation point
	The half-range of each chunk under extensive practice condition

Server 1. Equation Set VP-2: Eye movement modeling in picture information perception: Equation (3) (Lim & Liu, 2009)

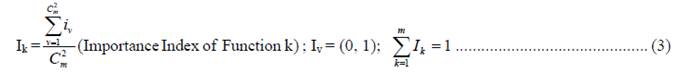
Variables
	Importance index of function k	The relatively important function can be given a value 1, and a value 0 is given to the other. The importance index of function k can be calculated.
	The importance value for function k	The importance value for function k obtained from each pair-wise comparisons, either 1 or 0.

Sever 3. Equation Set VP-3: Visual optical flow perception and speed perception: Equation (1) (Zhao & Wu, 2013)

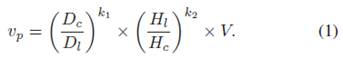
Variables
	Perceived speed
V	Actual speed
	The current texture density
	The texture density in the last driving scenario
	The eye height in the last driving scenario
	The current eye height
	two constant parameters

Sever 4. Equation Set VP-4: Visual detection modeling with detection distance and image matrix: Equation (12) (Bi, Tsimhoni, & Liu, 2009)

Variables
RPOT	Square root of the number of pixels on a target
f	Focal length
S	Size of the area of a target object.
D	Distance of the image forming

－Auditory perceptual subnetwork:

Sever 6. Equation Set AP-1: Modeling the effect of loudness on speech warning perception: Equation (1, 11) (Zhang, Wu, & Wan, 2016)

Variables
	The perceived urgency	Modeling the relationship between loudness and perceived urgency
,	Constants	The relationship between intensity and perceived urgency was quantified: = 1.33, = −0.64,
	Random factors	distributed random factors following distribution [0, 0.7]
L	Loudness level

Variables
	The effect of loudness on reaction time
	The initial entity processing time in Server 6
	The effect of loudness on perceived urgency

Sever 8. Equation Set AP-2: Modeling the effect of signal word on speech warning perception: Equation (12) (Zhang, Wu, & Wan, 2016)

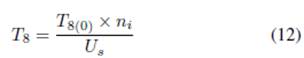
Variables
	The effect of signal word choice on reaction time
	The entity processing time in Server 8
	The urgency level expressed by the initial words
	The number of words in the ith speech warning

Cognitive Subnetwork

－Server B:

Equation Set C-1: Modeling of optimal chunking of textual information: Equation (22) (Wu & Liu, 2008b)

Variables	Description
Z	Objective function of task completion time
	Overall duration of processing each chunk at servers after server B
N	Total number of entities processed
x	Chunk size
	Rate of retrieval failure at server B
R	Average duration to correct an error caused by a wrongly processed entity or character

Equation Set C-2: Modeling of memory decay of speech information: Equation (7) ( Zhang, Wu, & Wan, 2016)

Variables	Description
	The probability of memory decay
	Lead time of a speech warning

Equation Set C-3: Modeling the probability of route choice in reinforcement learning of the speech warnings: Equation (4-5) ( Zhang, Wu, & Wan, 2016)

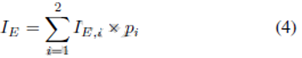
Variables
	The route choice error rate
	The error rate when a speech warning travels via route i
	The probability of a speech warning entity processed via route i

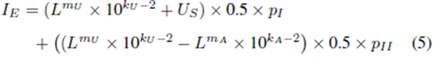
Variables
	The error rate of route choice
L	Loudness level in dB
	Perceived urgency level with different signal word choice
,	Parameters to quantify the power law of perceived urgency and loudness
,	Parameters to quantify the power law of perceived annoyance and loudness
pI, pII	Probabilities of choosing route I (the shorter route) and route II (the longer route)

－Server C:

Equation Set C-4: Inhibiting incompatible responses modeling: Equation (4-6) (Wu & Liu, 2008a)

Variables
T2,C-comp and T2,F-comp,	Processing times of Server C and F in the compatible conditions
T2,C-incomp and T2,F-incomp	Processing times of Server C and F in the incompatible conditions
SOA (stimulus onset asynchrony)	The delay between the presentation of the stimuli of T1 and T2
Tk	Processing time at server k (k=AP, VP, A, B, C, F, W, Y, Z, X)

Equation Set C-5: Dual task interference modeling: Equation (8-9) (Lin & Wu, 2012)

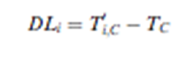
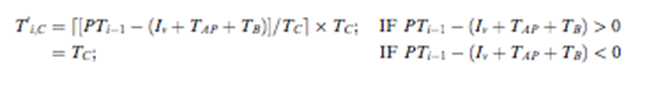
Variables	Description	Sources
DLi	Delay time
Ti,C	The entity processing time needed at Server C
PTi-1	Time lapse for the previous key to be pressed
Iv	Inter stimulus interval
Iv + TAP+ TB	Time lapse for the entity of the on-going stimulus to leave Server B
PTi-1-(Iv +TAP+TB)	The least duration that the current stimulus needs to wait at Server C
TC	Cycle time at Server C

－Server E:

Equation Set C-6: Background noise in motor control: Equation (15) (Lin & Wu, 2012)

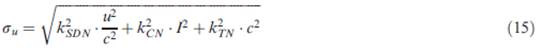
Variables
	The extent of SDN added with muscle activation level u;	Modelling baseline errors in numerical typing
,	Experimental constants	Modelling baseline errors in numerical typing
u	Muscle activation level	Modelling baseline errors in numerical typing
c	The extent of temporal noise	c is the extent of TN which accumulates as movement time increases
I	Interference index	I was an interference index accounting for the relative extent of the dual-task interference in background noise (CN).

－Server F

Equation Set C-7: Choice reaction modeling in multiple tasks: Equation (B16) (Wu & Liu, 2008a)

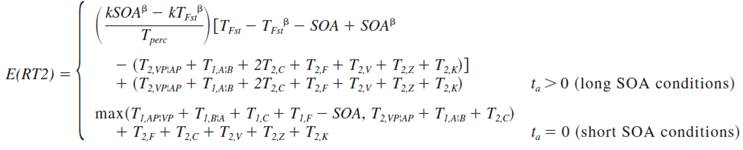
Variables
E(RT2)	Expected reaction time
SOA	Stimulus-onset asynchrony	The time difference between the onset of the two stimuli from two tasks
Ti	Processing time of servers see (Wu & Liu, 2008a)
TFst

Equation Set C-8: Modeling the effects of response complexity (using a single finger or multiple fingers at the same time): Equation (1-13) (Lin & Wu, 2012)

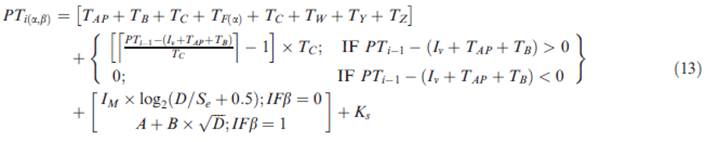
Variables
	Response time to i th stimulus with a finger strategy under an urgency condition
	Finger strategy
i	Response order
T	Processing time

Equation Set C-9: Complex decision making with value matrix: Equation (5) (Zhao & Wu, 2013)

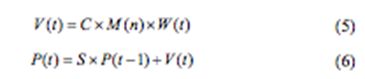
Variables
P(t)	Speed choice at time t
V(t)	Momentary valence
M(n)	Human subjective attribute matrix
W(t)	Attention weight matrix
S	Feedback matrix

Equation Set C-10: Perceived risk modeling: Equation (5) (Zhuang & Wu, 2013)

Variables
PRv	Human perceived risk increases with higher risk from vehicles
PRl	Human perceived risk increases with higher risk from local-defined risk
ag	A coefficient adjusting effect of group size of human
Ngroup	Group size of human

Equation Set C-11: Decision making in lateral control: Equation (1, 2) (Bi, Gan, Shang, & Liu, 2012)

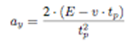
Variables
	Increment of steering angle
kp, kd	The coefficients of proportional derivative controller
a'y	The first derivative of acceleration
E	Error between the desired lateral position gained with the predefined desired path and predictive lateral position computed with the internal vehicle dynamics model
v	Current lateral velocity
tp	Preview time

Equation Set C-12: Modeling hazard evaluation accuracy: Equation (8, 16, 21) ( Zhang, Wu, & Wan, 2016)

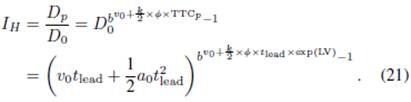
Variables
	The effect of hazard evaluation accuracy on error rate
	Perceived value of hazard
	Actual value of hazard
	Estimated distance
	Threshold of perceived distance
	Actual distance between the current position of warning receiving vehicle
v(t)	Instant speed	The instant speed (v) and acceleration (at) at time t is modeled in [23] as follows:
	Global optic flow rate of the textured ground surface	φ is the global optic flow rate of the textured ground surface, a proportion of speed as long as eye height is constant
k	Parameter	The parameter k is quantified by the annual mileage divided by a maximum value of annual mileage in general
	Perceived time-to-collision	The perceived time-to-collision (TTCp) will be affected by the existence of the lead vehicle. TTC is the actual time to collision that the vehicle will be able to avoid a collision without exceeding the assumed maximum deceleration
LV	Lead vehicle status	LV is a dichotomous variable of the lead vehicle in order to model the effect of the lead vehicle on TTCp (0 = without lead vehicle; 1 = with lead vehicle)
	Lead time of speech warning

－Server G:

Equation Set C-13: Urgency and Motivation Modeling: Equation (12) (Lin & Wu, 2012)

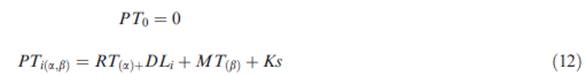
Variables
	Response time to i th stimulus with a finger strategy under an urgency condition
RT	Reaction time
DL	Delay time caused by dual-task interference
MT	Movement time
	Key-closure Time
	Finger strategy	notation of finger strategy. =0 →Single finger typing; =1 →Multi-finger typing
	Urgency	notation of urgency. =1→non-urgent condition; =0→urgent condition
i	Response order	notation of response order. i=1→first response in 9-digit number, and so on.

Motor Subnetwork

－Server W:

Equation Set M-1: Motor program retrieval modeling in the learning process: Equation (2) (Wu & Liu, 2008b)

Variables
	Processing time in each server	Reduction of Server Processing Time.
	Expected minimal processing time (Ti) at server i after intensive practice	Feyen (2002)
	Change in the expected processing time from the beginning to the end of practice	Reduction of Server Processing Time.
	Learning rate of server i	Heathcote et al. (2000)
	Number of entities processed by server i	Reduction of Server Processing Time.

－Server X:

Equation Set M-2: Error correction modeling in close-loop motor control: Equation (24-32) (Lin & Wu, 2012)

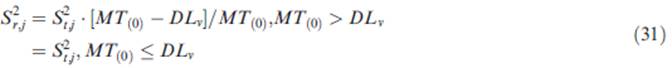
Variables
	The uncorrected portion of endpoint variability	Endpoint variability in different conditions
MT	Movement time	Modelling response time of numerical typing: the general equation of response time
DL	Delay time caused by dual-task interference	Modelling response time of numerical typing: the general equation of response time
Err%	Estimations of error rates	Estimations of error rates (Err%) in jth typing conditions
P(), P()	Parameters	The probability of errors in X-direction and Y-direction during jth experimental condition

－Hand Servers (Server 23, 24):

Equation Set M-3: Hand and finger movement time and errors in QWERTY keyboard typing: Equation (19) (Wu & Liu, 2008b)

Variables
Dis	Movement distance	Distribution of Movement Distance.
M	Population size	Equation (19) can be used to estimate the distribution of movement distance of different body parts including hands and fingers.
RD	Movement radius	Equation (19) can be used to estimate the distribution of movement distance of different body parts including hands and fingers.

Equation Set M-4: Bimanual (two hands) coordination: Equation (31-34), (Wu & Liu, 2008b)

Variables
Y	Time	The time (Y) saved by optimization of EPD
EPD	Error Prevention Duration	The optimization process of EPD is a trade-off between the time in typing and the time in error correcting
N	Number	The number of characters typed
	Parameter	It specifies how long to correct one transposition error
e	Parameter	It refers to the error rate of the transposition error made by reducing of EPD

Equation Set M-5: Hand and finger movement time and error in numerical typing: Equation (13) (16) (Lin & Wu, 2012)

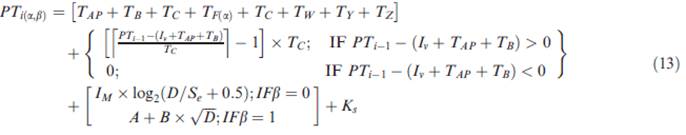
Variables
	Response time to ith stimulus with a finger strategy under β urgency condition	Modelling response time of numerical typing: the general equation of response time
	The processing time of ith stimulus at Server k	All Tk are estimated based on parameter settings in QN-MHP
D	Travel distance	Modelling baseline response time in numerical typing
	Effective target size	The effective target size (Se) is calculated based on the maximal target width that can be utilized without touching adjacent keys:
	Constant	Im =100 is used as it was suggested in the original study (Card et al. 1983)
	Key-closure Time	Modelling response time of numerical typing: the general equation of response time

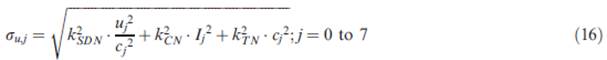
Variables	Description
	The Extent of SDN added with muscle activation level u in theexperimental condition
	Muscle activation level in theexperimental condition
	Extent of TN in theexperimental condition
	Interference index
,	Experimental constants

－Foot Server (Server 25)

Equation Set M-6: Movement time of foot in pressing a pedal: Equation (21) (Wu & Liu, 2008b)

Variables	Description	Sources
MT	Movement time	The foot server executes the simulated movement to press a pedal and its movement time () can be estimated by the formula proposed by Drury[1975]
S	Shoe width	S refers to the shoe width [10cm, Armstrong 2004]
W	Pedal width	W is the pedal width (10cm, same with the shoe width)
A	Parameter	A stands for the movement distance (3cm, typical movement distance for a foot pedal).

Equation Set M-7: Angular speed of the foot movement without considering the human personality as a factor of individual difference: Equation (3) (Zhao, Wu, & Qiao, 2013)

Variables	Description	Sources
	Pedal angular velocity	Mathematical Model of Human operator Speed Control: Speed Adjustment
A	Constant	Mathematical Model of Human operator Speed Control: Speed Adjustment
	Target speed	Mathematical Model of Human operator Speed Control: Speed Adjustment
	Perceived speed	Mathematical Model of Human operator Speed Control: Speed Adjustment

Equation Set M-8: Angular speed of the foot movement considering the human personality as a factor of individual difference (Zhao & Wu, 2013)

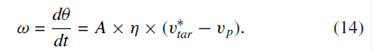
Variables	Description
	Pedal angular velocity
A	Constant
	Target speed
	Perceived speed
η	Personality index

Equation Set M-9: Effects of target speed of human on the vehicle movement speed : Equation (6) (Zhao & Wu, 2013)

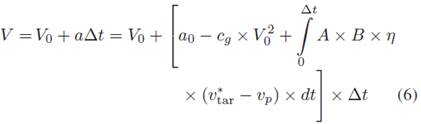
Variables	Description	Sources
V	Vehicle speed	Mathematical Model of Human operator Speed Control: Vehicle Mechanics
	Vehicle acceleration	Mathematical Model of Human operator Speed Control: Vehicle Mechanics
vtar	Target speed of a human operator
	Initial acceleration	Mathematical Model of Human operator Speed Control: Vehicle Mechanics
	Coefficient of the overall drag on the vehicle	Mathematical Model of Human operator Speed Control: Vehicle Mechanics
A,B	Constants	Mathematical Model of Driver Speed Control: Vehicle Mechanics

5. Major Contributors and Key Users of Mathematical Modeling of Human Performance using QN-MHP

We specially thank Dr. Yili Liu at University of Michigan who laid the theoretical foundation of queuing network modeling of human performance, unifying existing reaction time models using queuing network theory.

Dr. Changxu Wu (Group Coordinator) at University of Arizona, USA

Dr. Robert Feyen, University of Minnesota, USA

Dr. Omer Tsimhoni, General Motors, USA

Dr. Ji Hyoun Lim, Apple, USA; Hongik University, Korea

Dr. Luzheng Bi at Beijing Institute of Technology, China

Dr. Shi Cao at University of Waterloo, Canada

Dr. Guozhen Zhao at Chinese Academy of Sciences, China

Dr. Cheng-Jhe (Robert) Lin, National Taiwan University of Science and Technology

Dr. Jingyan Wan, General Motors, USA

Dr. Yiqi Zhang at Pen State University, USA

To become a member (user or contributor) of mathematical modeling group in human performance modeling, please email to changxu.wu@gmailcom (Please list your full name and institution/company name), we will send you recent updates, new modeling work, and new tutorials. All of them are free.

Reference

Bi, L., Gan, G., Shang, J., & Liu, Y. (2012). Queuing Network Modeling of Driver Lateral Control With or Without a Cognitive Distraction Task. IEEE Transactions on Intelligent Transportation Systems, 13(4), 1810 to 1820. doi:10.1109/TITS.2012.2204255

Bi, L., Tsimhoni, O., & Liu, Y. (2009). Using Image-Based Metrics to Model Pedestrian Detection Performance With Night-Vision Systems. IEEE Transactions on Intelligent Transportation Systems, 10(1), 155 to 164. doi:10.1109/TITS.2008.2011719

Cao, S., & Liu, Y. (2015). Modelling workload in cognitive and concurrent tasks with time stress using an integrated cognitive architecture. International Journal of Human Factors Modelling and Simulation, 5(2), 113 to 135.

Lim, J. H., & Liu, Y. (2009). Modeling the Influences of Cyclic Top-Down and Bottom-Up Processes for Reinforcement Learning in Eye Movements. IEEE Transactions on Systems, Man, and Cybernetics - Part A: Systems and Humans, 39(4), 706 to 714. doi:10.1109/TSMCA.2009.2018635

Lin, C.-J., & Wu, C. (2012). Mathematically modelling the effects of pacing, finger strategies and urgency on numerical typing performance with queuing network model human processor. Ergonomics, 55(10), 1180 to 204. doi:10.1080/00140139.2012.697583

Wu, C., Berman, M., & Liu, Y. (2010). Optimization in Brain? - Modeling Human Behavior and Brain Activation Patterns with Queuing Network and Reinforcement Learning Algorithms. In W. Chaovalitwongse, P. M. Pardalos, & P. Xanthopoulos (Eds.), Computational Neuroscience (Vol. 38, pp. 157 to 179). New York, NY: Springer New York. doi:10.1007/978-0-387-88630-5

Wu, C., & Liu, Y. (2007). Queuing Network Modeling of Driver Workload and Performance. Intelligent Transportation Systems, IEEE Transactions on, 8(3), 528 to 537.

Wu, C., & Liu, Y. (2008a). Queuing network modeling of the psychological refractory period (PRP). Psychological review, 115(4), 913 to 954. doi:10.1037/a0013123

Wu, C., & Liu, Y. (2008b). Queuing network modeling of transcription typing. ACM Transactions on Computer-Human Interaction, 15(1).

Wu, C., Liu, Y., & Quinn-Walsh, C. M. (2008). Queuing Network Modeling of a Real-Time Psychophysiological Index of Mental Workload-P300 in Event-Related Potential (ERP). Systems, Man and Cybernetics, Part A: Systems and Humans, IEEE Transactions on, 38(5), 1068 to 1084.

Wu, C. (2016). The Five Key Questions in Human Performance Modeling. International Journal of Industrial Ergonomics, Accepted.

Zhao, G., & Wu, C. (2013). Mathematical Modeling of Driver Speed Control With Individual Differences. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 43(5), 1091 to 1104. doi:10.1109/TSMC.2013.2256854

Zhao, G., Wu, C., & Qiao, C. (2013). A Mathematical Model for the Prediction of Speeding with its Validation. IEEE Transactions on Intelligent Transportation Systems, 14(2), 828 to 836.

Zhang, Y., Wu, C., & Wan, J. (2016). Mathematical Modeling of the Effects of Speech Warning Characteristics on Human Performance and Its Application in Transportation Cyberphysical Systems. IEEE Transactions on Intelligent Transportation Systems, 17(11), 3062 to 3074.

Zhuang, X., & Wu, C. (2013). Modeling Pedestrian Crossing Paths at Unmarked Roadways. IEEE Transactions on Intelligent Transportation Systems, 14(3), 1438 to 1448.